여러 실험을 통해 관찰된 바에 따르면 동일한 축력으로 여러 개의 같은 강철 막대와 고무를 잡아당기면 이 두 막대에는 서로 다른 신장이 발생한다. 역학에서 두 막대의 재질의 차이는 응력과 변형도의 성분들 사이의 관계에 의해 표현된다. 이러한 각 항목을 열 행렬로 표현하면 다음과 같다.
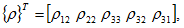(1)
(2)
여기서 우리는 다음 사항을 얻는다.
(3)
이때 X는 본체의 재질을 특징짓는 5 × 5 행렬이며 일반적으로 탄성 행렬로 알려져 있다. 이 행렬의 원소들은 본체 재질을 위한 탄성력 또는 탄성 상수라고 불린다. 전단 변형률은 수식 (2)에 2를 곱한 것이며, 정의 (1)과 (2)는 
을 보장한다. 수식 (3)에 표시된 응력과 변형도 사이의 관계를 본체 재질에 대한 구성 관계라고 한다. 수식 (3)에서는 변형도 d가 측정되는 참조 구성에 따라 본체가 무응력 상태라고 가정한다.
It is observed from frequent experimentation that drawing identical bars from steel and rubber by same axial force and consequently the same axial stress, results in different elongations from the two bars. In mechanics, the differences of the two bars is represented by the relationship between the components of stress and strain. The writing of these like a matrix of column, i.e
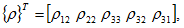(1)
(2)
we have
(3)
where X is a 5 x 5 matrix that characterizes the material of the body, and is generally called the matrix of elasticity and its components are called elasticity’s or constants of elasticity for the material of the body. Note that shear strains have been multiplied by 2 in eqn. (2); the definitions (1) and (2) make sure that . The equation (3), in other words the relation between the stresses and strains, are called the relation constitutive for the material of the body. It is assumed in Eq. (3) that the body is stress free in the configuration of reference from which the strain d is measured.
このページでは、クロスチェッカーやネイティブチェッカー（校正者）が加えた修正変更を分かりやすいように色付きで紹介していますが、通常お客様には、修正変更履歴を残さず、最終版のみを納品しております。
It is observedfrom frequent experimentation that drawing pulling 1identicalbars from steeland rubber by the same axial force,and consequentlythe sameaxial stress, results of stress indifferent elongations from the two bars. In mechanics, the differences difference inthe materials 2of the two bars is represented by the relationship betweenthe components of stress and the strain. TheBywriting each ofthese likeasa matrix of column matrix,i.e.,3
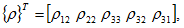(1)
(2)
we have
(3)
where X is a 5 x 5 matrix that characterizes thematerial of the body, and is generallycalled the matrix of elasticityand itscomponents are called elasticity’s elasticities 4or elastic constantsof elasticity 5for the material of the body.Note that shear strains have been multiplied by 2 in eqn. (2); the definitions (1) and(2) make ensure6 that. Theequation (3), in other words the relation between the stresses and strains, areiscalled the relationconstitutive relation for the material of the body.It is assumed in Eq. (3) that the body is stress free in the reference configuration of reference from which the strain d is measured.
It is observed from fFrequent1experimentation has shown that drawing pulling 2the identical barsof from steel and rubber having the same initial lengths by the sameaxial force, and consequently thus thesame axial stress, results ofstress in different elongations from of these two bars. In mechanics, the differences difference in the materials 3of the two bars is represented by the relationship betweenthe components of stress and the strain.TheBywritingexpressing 4each of these likeasa matrix of column matrix5,i.e.,6
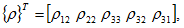(1)
(2)
we haveobtain
(3)
whereHere,X is a 57 x× 5 matrix that characterizes thematerial of the body,and is generally. It is generally calledknown asthe matrix of elasticity andmatrix;8 itscomponents are called elasticity’s elasticities 9or elastic constants10of elasticity forthe material of the body. Note thatThe shear strains have been multiplied by 2 in eqn.Eq. (2); the definitions (1)and (2) makeensure11 that. Thestress-strainequation (3), in other words the relation shown inbetween the stresses and strains, are Eq. (3) is called known as therelation constitutiverelationfor the material of the body. 12It is assumed in Eq. (3) that thebody is stress-13free in the reference configuration of reference fromwhich the strain d is measured.
Frequent experimentation has shown that pulling the bars of steel and rubber having the same initial lengths by the same axial force, and thus the same axial stress, results in different elongations of these two bars. In mechanics, the difference in the materials of the two bars is represented by the relation between the components of stress and strain. By expressing each of these as a column matrix, i.e.,
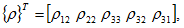(1)
(2)
we have
(3)
Here, X is a 5 × 5 matrix that characterizes the material of the body. It is generally known as the elasticity matrix; its components are called elasticities or elastic constants for the material of the body. The shear strains have been multiplied by 2 in Eq. (2); definitions (1) and (2) ensure that . The stress–strain relation shown in Eq. (3) is known as the constitutive relation for the material of the body. It is assumed in Eq. (3) that the body is stress-free in the reference configuration from which the strain d is measured.
